Вступление
Я применил обобщение к принцип включения-исключения, который распространяет принцип от множеств на более общие объекты. Короче говоря, принцип вычисляет левую, выполняя вычисления справа.
Чтобы распространить это на общие объекты, эти объекты должны иметь некоторые structure (какое-то определяющее свойство). Им нужно иметь представление о intersection (что общего между двумя объектами) и, наконец, понятие cardinality (размер или питонами длина). Символ пересечения — ∩, а мощность | | используется.
Итак, этот код делает именно это. Он создает объекты, которые имеют понятие пересечения, мощности, а затем использует принцип включения-исключения для вычисления размера (мощности) их объединения (| AUBU .. |).
Требуется обратная связь
Мой код работает, но я получаю некоторые ошибки с подсказками, так как не знаю, как аннотировать IEP учебный класс. Так что отзывы о том, как реализовать правильные подсказки для набора текста, более чем приветствуются.
Говоря об IEP, я чувствую, что вся моя конструкция объектов надумана. Я хочу некий общий метакласс, который снова производит IEP объекты, у которых есть набор intersection и cardinality. Это то, что make_IEP do, но опять же, размещение класса внутри функции кажется нелогичным.
Код
utilities.py
from collections.abc import Iterable, Callable
from typing import Any, TypeVar, Tuple, Union
import functools
import itertools
_T = TypeVar("_T")
_S = TypeVar("_S")
@functools.cache
def reduce_w_cache(function: Callable[[_T, _S], _T], sequence: Iterable[_S]) -> _S:
"""Reduces the sequence to a single number by left folding function over it
Example:
The easiest way to understand how reduce works is applying a tuple to it
>>> sequence = tuple([1, 3, 5, 6, 2])
>>> make_tuple = lambda x, y: tuple([x, y])
>>> reduce_w_cache(make_tuple, sequence)
((((1, 3), 5), 6), 2)
Similarly a right fold would look like ``(1, (3, (5, (6, 2))))``
>>> add = lambda x, y: x + y
>>> sum_reduce = lambda x: reduce_w_cache(add, x)
>>> reduce_w_cache(add, sequence)
17
Understanding how this works is as easy as replacing , with + in the
example above
reduce_w_cache(add, sequence) = ((((1 + 3) + 5) + 6) + 2) = 17
Let us test if the caching works. We first save how many misses we
have, where a miss corresponds to a value being added to the cache. We
will then perform some lookups and study how many values were cached.
>>> repeat_reduce = lambda fun, seqs: [reduce_w_cache(fun, tuple(s)) for s in seqs]
>>> def values_cached(function, sequences):
... initial = reduce_w_cache.cache_info().misses
... repeat_reduce(function, sequences)
... total = reduce_w_cache.cache_info().misses
... return total - initial
>>> test_function = lambda x, y: [x, y]
>>> sequences = [
[103], [103, 105], [103, 105, 107], [103, 105, 107, 109], [103, 105, 107, 109, 111]
]
We are going to run ``reduce_w_cache`` with ``test_function`` over each
element in ``sequences``. With no caching we would expect ``len - 1``
function calls with a minimal of ``1`` for each sequence in sequences.
Totaling to ``1 + 1 + 2 + 3 + 4 = 11`` function calls.
However with cached values this is greatly lowered. For instance ``(103,
105, 107)`` folds to ``(103, (105, 107))`` and the value of
``(105, 107)`` is already stored in the cache.
>>> values_cached(test_function, sequences)
5
No new values should be added if we lookup the same values again
>>> values_cached(test_function, sequences)
0
As a sanity check let us test how many values are cached when
we can not use previously stored values
>>> sequences = [
[112], [113, 114], [115, 116, 117], [118, 119, 120, 121], [118, 119, 120, 121, 122]
]
>>> values_cached(test_function, sequences)
11
Let us double check that the number of calls really is 11. For each
function call we wrap two elements in ``[]`` so simply counting the number
of either ``[`` or ``]`` returns the number of function calls.
>>> str(repeat_reduce(test_function, sequences)).count('[')
11
"""
*remaining, last = sequence
if not remaining:
return last
return function(reduce_w_cache(function, tuple(remaining)), last)
def powerset(iterable:Iterable[Any], emptyset:bool=False, flatten:bool=True) -> Iterable[Union[Tuple[Any, ...],Iterable[Tuple[Any, ...]]]]:
"""Returns the powerset of some list without the emptyset as default
Examples:
>>> list(powerset([1,2,3]))
[(1,), (2,), (3,), (1, 2), (1, 3), (2, 3), (1, 2, 3)]
>>> list(powerset([1,2,3], emptyset=True))
[(), (1,), (2,), (3,), (1, 2), (1, 3), (2, 3), (1, 2, 3)]
>>> list(list(i) for i in powerset([1,2,3], flatten=False))
[[(1,), (2,), (3,)], [(1, 2), (1, 3), (2, 3)], [(1, 2, 3)]]
>>> list(list(i) for i in powerset([1,2,3], emptyset=True, flatten=False))
[[()], [(1,), (2,), (3,)], [(1, 2), (1, 3), (2, 3)], [(1, 2, 3)]]
"""
try:
iter(iterable)
s = list(iterable)
except TypeError:
if not isinstance(iterable, list):
raise TypeError("Input must be list or iterable")
s = iterable
start = 0 if emptyset else 1
powerset_ = (itertools.combinations(s, r) for r in range(start, len(s) + 1))
return itertools.chain.from_iterable(powerset_) if flatten else powerset_
if __name__ == "__main__":
import doctest
doctest.testmod()
iep.py
"""
Provides a module for the inclusion exclusion protocol
"""
from collections.abc import Callable
import functools
from typing import Annotated, Any, Union, Type
from utilities import powerset, reduce_w_cache
Structure = Annotated[
Any,
"An intrinsic property that defines the shape and form of our object",
]
Intersection = Annotated[
Callable[[Structure, Structure], Structure],
"Is a callable function that takes in two structures and returns the"
"intersection, which is a new (smaller or equal) structure.",
]
# Defines an empty class here for typing hints
class IEP:
def __init__(self, structure: Structure):
self.structure = structure
pass
Cardinality = Annotated[
Callable[[Type[IEP]], Union[int, float]],
"Is a callable function that returns the general concept of size for an object",
]
class ConstructorIEP:
"""Implements intersection and cardinality (len) for the IEP class"""
def cardinality(self, x):
return x
def intersect(self, x, _):
return x
@property
def structure(self):
return self._structure
@structure.setter
def structure(self, stuff: Structure):
self._structure = stuff
self.len = self.cardinality(self._structure)
def intersection(self, *others: Type[IEP]):
if len(others) == 0:
new_structure = self.structure
new_structure = self.structure
for other in others:
new_structure = self.intersect(new_structure, other.structure)
NewIEP = make_IEP(self.intersect, self.cardinality)
return NewIEP(new_structure)
def __len__(self):
return self.len
def __repr__(self):
return f"IEP({self.structure})"
def __str__(self):
return f"{self.structure}, len={self.len}"
def make_IEP(intersect: Intersection, cardinality: Cardinality) -> Type[IEP]:
"""Creates an IEP class with a fixed intersect and cardinality"""
class IEP(ConstructorIEP):
def __init__(self, structure: Structure):
self.intersect = intersect
self.cardinality = cardinality
self.structure = structure
return IEP
def inclusion_exclusion_principle(
structure_of_objects: list[Structure],
intersection_: Intersection,
cardinality_: Cardinality,
cache: bool = False,
) -> int:
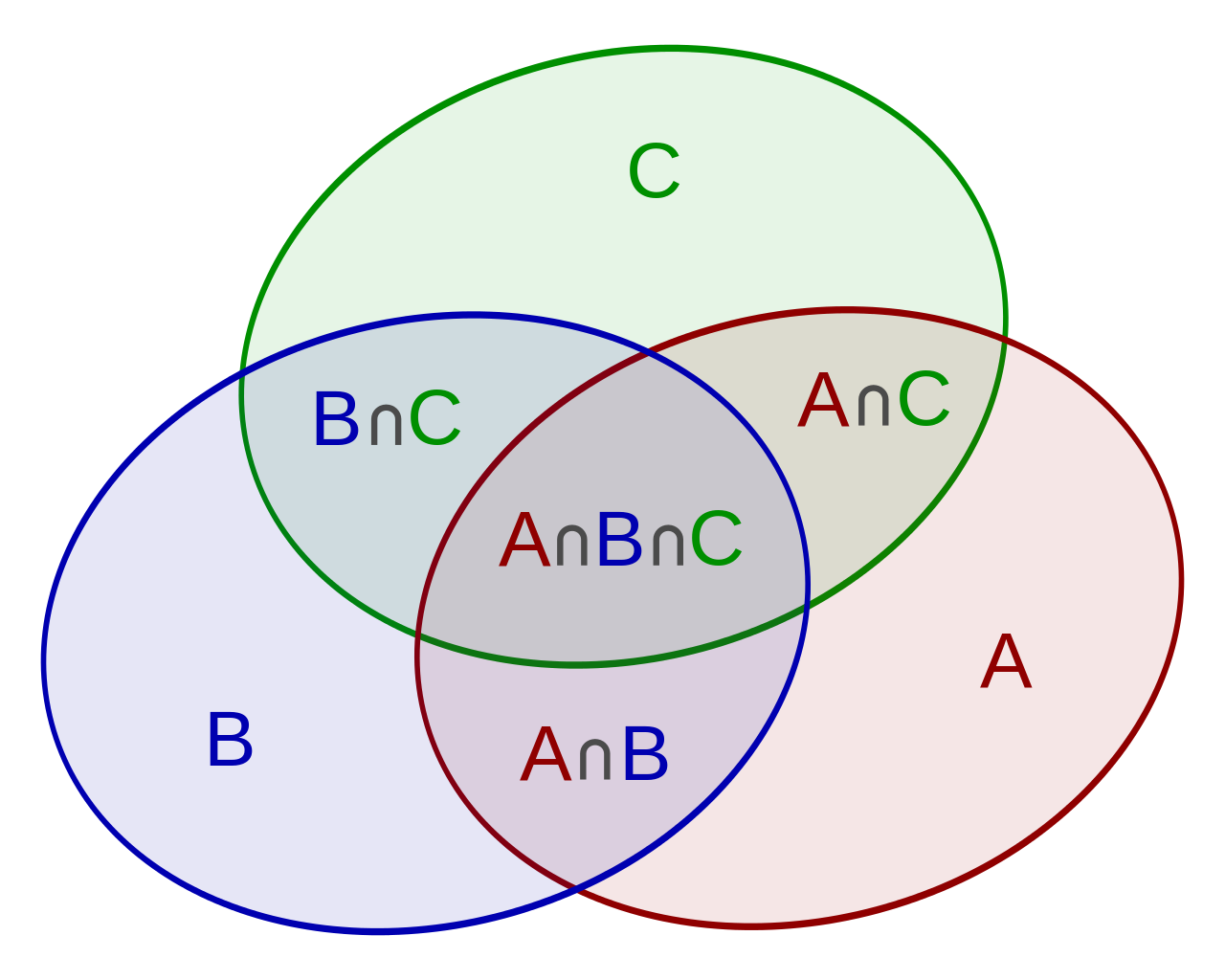
"""If structure_of_objects = [A, B, C, ...] this function returns |A U B U C U ...|
The return value is calculated using the exclusion inclusion principle;
here | | denotes the cardinality (or in Pythons words the length) of the set,
and ∩ represents the intersection of two objects, and U representens the union.
See the link for more information
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
Args:
structure_of_objects: A list of structures that with intersection and
cardinality defines an object
intersection: A function(x, y) that returns what two object structures has
in common (defines x.intersection(y))
cardinality: A function(x) that returns the size of an object (defines len(object))
Returns:
int: Returns the size (``len``) of the intersection of every element in ``list_of_objects``
Examples:
Setup for discrete sets
>>> intersection = lambda a, b: a.intersection(b)
>>> cardinality = len
>>> sets = [set([])]
>>> inclusion_exclusion_principle([{}], intersection, cardinality)
0
>>> inclusion_exclusion_principle([{1, 2, 3}, {1, 2, 3}], intersection, cardinality)
3
>>> inclusion_exclusion_principle([{1, 2, 3}, {4, 5, 6}], intersection, cardinality)
6
Setup for continous ranges is a bit harder as it is cumbersome to define the
intersections between two intervals properly
>>> def intersection(*intervals):
... max_first, min_last = [f(i) for f, i in zip([max, min], zip(*intervals))]
... if (min_last - max_first) >= 0:
... return [max_first, min_last]
... return [float("inf"), float("inf")]
...
>>> cardinality = lambda a: len(range(*a))
>>> inclusion_exclusion_principle([[0, 0]], intersection, cardinality)
0
>>> inclusion_exclusion_principle([[1, 2], [1, 2]], intersection, cardinality)
1
>>> inclusion_exclusion_principle([[0, 3], [1, 2]], intersection, cardinality)
3
>>> inclusion_exclusion_principle([[2, 4], [3, 5], [4, 6]], intersection, cardinality)
4
As a more advanced example we can use inclusion-exclusion-principle to
find the union of all numbers divisible by 1 or more of our objects.
Essentially solving the first project euler problem
>>> gcd = lambda m,n: m if not n else gcd(n, m % n)
>>> lcm = lambda a, b: abs(a * b) // gcd(a, b)
>>> start, stop = 1, 1000
>>> intersection = lcm
>>> cardinality = lambda x: sum(i for i in range(start, stop) if i % x == 0)
>>> inclusion_exclusion_principle([3, 5], intersection, cardinality)
233168
Of course this could have been improved by implementing a cardinality
that runs in linear time
>>> sum_linear = lambda start, stop: (stop + start + 1) * (stop - start) // 2
>>> cardinality = lambda x: x * sum_linear(start//x, (stop-1)//x)
>>> inclusion_exclusion_principle([3, 5], intersection, cardinality)
233168
"""
class IEP(ConstructorIEP):
def __init__(self, structure: Structure):
self.intersect = intersection_
self.cardinality = cardinality_
self.structure = structure
list_of_objects = list(map(IEP, structure_of_objects))
reduce = reduce_w_cache if cache else functools.reduce
def intersect(list_of_objects: list[Type[IEP]]):
"""Finds the intersection of a list of objects according to the rules set by intersection"""
# If the list of sets only contains one element, we are left with
# finding the intersection of a set with itself. However, this is just
# the set itself, because intersection retrieves the common elements.
# Here, all elements of a set is common with itself. Hence, the
# resulting intersection of a set with itself, is itself
if len(list_of_objects) == 1:
return list_of_objects[0]
return reduce(lambda x, y: x.intersection(y), list_of_objects)
def cardinality(obj):
return len(obj)
cardinality_of_union, sign = 0, 1
# It will be easier to follow this code through an example
# list_of_objects = [A, B, C]
# powerset(list_of_objects, flatten=False) = [
# [[A], [B], [C]],
# [[A, B], [A, C], [B, C]],
# [A, B, C]]
# ]
for subsets_w_same_len in powerset(list_of_objects, flatten=False):
# intersections:
# First pass: = [A, B, C] # All subsets of len 1 (intersection of itself is itself)
# Second pass: = [A ∩ B, A ∩ C, B ∩ C] # All subsets of len 2
# Final pass: = [A ∩ B ∩ C] # All subsets of len 3
intersections = map(intersect, subsets_w_same_len)
# cardinalities:
# First pass: = [ |A|, |B|, |C| ]
# Second pass: = [ |A ∩ B|, |A ∩ C|, |B ∩ C| ]
# Final pass: = [ |A ∩ B ∩ C| ]
cardinalities = map(cardinality, intersections)
# cardinality_of_union:
# First pass: = |A| + |B| + |C|
# Second pass: = |A| + |B| + |C|
# - ( |A ∩ B| + |A ∩ C| + |B ∩ C| )
# Final pass: = |A| + |B| + |C|
# - ( |A ∩ B| + |A ∩ C| + |B ∩ C| )
# + ( |A ∩ B ∩ C| )
cardinality_of_union += sign * sum(cardinalities)
sign *= -1
# Where
# cardinality_of_union = |A| + |B| + |C|
# - ( |A ∩ B| + |A ∩ C| + |B ∩ C| )
# + ( |A ∩ B ∩ C| )
# = |A U B U C |
# By the inclusion excluion principle, which is what we wanted
return cardinality_of_union
if __name__ == "__main__":
import doctest
doctest.testmod()
1 ответ
reduce_w_cacheСклонен к достижению пределов рекурсии. Вы должны использовать итеративный подход, а не функциональный.
>>> reduce_w_cache(int.__add__, (1,) * 1000) Traceback (most recent call last): File "<stdin>", line 1, in <module> File "<stdin>", line 6, in reduce_w_cache File "<stdin>", line 6, in reduce_w_cache File "<stdin>", line 6, in reduce_w_cache [Previous line repeated 496 more times] RecursionError: maximum recursion depth exceededНе работает с последовательностью 0. Условием является предоставление kwarg по умолчанию, например;
max,min,dict.get.>>> max([], default=0) 0Ваша функция медленная $ O (п ^ 2) $ вы можете получить (амортизировать) $ O (п) $ производительность путем создания кеша самостоятельно. Самый простой и наивный (он же сломанный) подход может быть таким:
Сохраните размер кеша. Это избавляет нас от необходимости разрезать ввод (получение $ O (п ^ 2) $ время).
Итеративно создайте кеш. Предположим, мы используем
reduce_w_cacheчтобы хешировать последовательность, вы должны заметить, что мы можем просто построить предыдущий хеш.
_hash = 0 for size, value in enumerate(sequence, 1): _hash ^= hash(value) cache[size, _hash] = ...Чтобы алгоритм работал, вам нужно правильно обрабатывать коллизии (сложная часть построения хеш-карты). Вы должны сохранить оригинал в ключе, но не использовать его для сравнения значений. Если размер и хэш совпадают, вам нужно использовать его для сравнения коллизий с помощью $ O (nk) $ алгоритм. Где $ n $ размер значения и $ k $ количество столкновений.
Чтобы уменьшить количество столкновений, вам нужно принять во внимание проблему дня рождения, что может привести к небольшому потреблению памяти.
В целом я думаю
functools.reduceбыло бы лучше здесь.powersetО том, что я ожидаю от функции powerset.
я думаю
flatten— плохой дизайн и делает вашу функцию подходящей для превращения в функцию бога.powerset(..., flatten=True)против
flatten = itertools.chain.from_iterable flatten(powerset(...))«Входные данные должны быть списковыми или повторяемыми» и
isinstance(iterable, list)странные какlistявляется повторяемый. Вероятно, вы можете просто удалить код.>>> import collections.abc >>> issubclass(list, collections.abc.Iterable) True
IEPДолжен быть протокол.
IEPдолжен называтьсяIIEP, ну что-нибудь кромеIEP. ДополнительныеIявляется номенкультура взята из C # означает «Интерфейс».Самым большим преимуществом, и почему я скопировал стиль из C #, является отсутствие повторяющихся имен для интерфейса и реализации.
ConstructorIEPСмотрится неплохо. Но есть некоторые придирки.
Мне не нравятся чертовы методы внизу вашего класса. Несмотря на то, что у него четкий стиль, заслуживает всяческой похвалы.
Вот мой стиль:
Подсказки типа.
Конструкторы.
__new____init__- Классовые или статические построители.
Методы Dunder
Все остальное
Я классифицирую вспомогательные функции, которые нужно сгруппировать с исходной функцией. Скажем, у вас есть метод dunder, который становится немного большим, разделение функции на два метода (один dunder один нормальный) не должно перемещать обычный метод в конец класса.
intersectionвыглядит немного странно.if len(others) == 0: new_structure = self.structure new_structure = self.structureВаш str dunder должен позвонить
__len__не искатьlen. Делает ваш код более Pythonic и позволяет подклассам следовать идиомам Python, при этом код по-прежнему работает нормально.
make_IEPЯ думаю, что функция должна быть построителем классов на
ConstructorIEP.Я не фанат
self.intersect = intersect. Привяжите метод к классу, а не к экземпляру.@classmethod def build_type(cls, intersect: Intersection, cardinality: Cardinality) -> Type[IEP]: """Creates an IEP class with a fixed intersect and cardinality""" class IEP(ConstructorIEP): intersect = staticmethod(intersect) cardinality = staticmethod(cardinality) def __init__(self, structure: Structure): self.structure = structure return IEP
inclusion_exclusion_principle(не полный обзор)intersection_должно бытьintersectionиintersectionдолжно бытьintersection_. Пользователю вашей функции наплевать, каковы внутренние имена вашей функции, но делать позаботьтесь о разумных именах аргументов.Почему вы определили
IEPснова и не используетсяmake_IEP?
Я не математик, поэтому остановлюсь на этом.
В целом мой ответ — в основном придирки или несколько тривиальные лакомые кусочки. Хороший код.

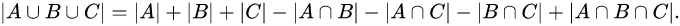
Я никогда не знал, что смогу подтолкнуть конструктора классов к
ConstructorIEP! =) Аналогичноstaticmethodбыл недостающей частью, я попытался привязать методы к классу, а не к экземпляру, но не смог заставить его работать. Причина, по которой IEP была определена снова, — это остаток кода после попытки рефакторинга (хотелось удалитьmake_IEP).— N3buchadnezzar
Как после мысли мне нужно
ConstructorIEPучебный класс? Или я мог бы просто засунуть все вbuild_typeфункция? Кажется немного странным, чтоIEPнаследуетbuild_typeclassmethod.— N3buchadnezzar
@ N3buchadnezzar Я не вижу ничего плохого в том, чтобы иметь
ConstructorIEPкоторый строит новый тип. В конце концов, строитель — это просто вспомогательный метод. Если ваш код становится более сложным, то полагаться на вспомогательный метод для основных функций может быть плохо, но нам нужно знать ситуацию, чтобы на самом деле прокомментировать, является ли подход неоптимальным. Вы можете попробовать другие методы, чтобы делать то, что хотите, но если все подходы работают оптимально, в чем проблема? Тем не менее, я считаю метапрограммирование довольно ненормальным и не следует «нормальным» процессам.— Пейлонрайз♦