Я написал код на Python, чтобы определить результат (включая оставшиеся войска обеих сторон) битвы за риск, пока одна из сторон не будет побеждена. При использовании njit-декоратора Numba код может имитировать исход одного боя за ~ 0,2 мс. Это недостаточно быстро для приложения, которое я имею в виду. В идеале это было бы на один-два порядка быстрее. Мы будем очень благодарны за любые советы о том, как улучшить производительность.

Код функции:

@njit
def _attack_(n_atk,n_def):
    n_atk_dies = 0
    n_def_dies = 0
    while n_atk >0 and n_def>0:
        if n_atk>=3:
            n_atk_dies = 3
        if n_atk==2:
            n_atk_dies = 2
        if n_atk ==1:
            n_atk_dies = 1
        if n_def >=2:
            n_def_dies = 2
        if n_def ==1:
            n_def_dies = 1   
        atk_rolls = -np.sort(-np.random.randint(1,7,n_atk_dies))
        def_rolls = -np.sort(-np.random.randint(1,7,n_def_dies))
        comp_ind = min(n_def_dies,n_atk_dies)
        comp = atk_rolls[:comp_ind]-def_rolls[:comp_ind]
        atk_losses =len([1 for i in comp if i<=0])
        def_losses = len([1 for i in comp if i>0])
        n_atk -= atk_losses
        n_def -= def_losses
    return [n_atk,n_def]

Код сравнительного анализа:

atk_list = list(np.random.randint(1,200,10000))
def_list = list(np.random.randint(1,200,10000))
cProfile.run('list(map(_attack_,atk_list,def_list))',sort="tottime")

Вы играете, используя до 199 кубиков на игрока. Таким образом, в большинстве случаев атакующий будет атаковать 3 кубиками, а защищающийся — 2 кубиками. Если это так, вы можете просто выбрать один из трех возможных результатов (с заранее рассчитанными вероятностями) и применить его. Контур:

def _attack_(n_atk,n_def):
    while n_atk >= 3 and n_def >= 2:
        # pick random outcome and update the dice numbers
    while n_atk >0 and n_def>0:
        # same as before
    return [n_atk,n_def]

Вы даже можете предварительно вычислить распределения результатов для всех $ 199 ^ 2 $ возможные входы и случайным образом выбираем результат в соответствии с заданным распределением входных данных. Контур:

def _attack_(n_atk,n_def):
    return random.choices(results[n_atk, n_def], cum_weights=cum_weights[n_atk, n_def])

Я не тестировал ни одно из следующего, но подозреваю, что они могут вам помочь. Каждую переделку проверял отдельно.

Во-первых, выбор количества игральных костей (кубик — единственное число, кубик — множественное число) сбивает с толку и, вероятно, медлителен.

n_atk_dice = min(n_atk, 3)
n_def_dice = min(n_def, 2)

Во-вторых, используя np.sort является (а) излишним для проблемы и (б) вероятно медленным, поскольку вам нужно перейти в другую библиотеку, чтобы сделать это. Что я имею в виду под «излишним»? Общие алгоритмы сортировки должны работать для списков любой длины. Но есть оптимальные алгоритмы сортировки для любой фиксированной длины списка. Поднимая мой Искусство программирования, Том 3, мы можем написать следующее:

def sort2(l):
    if l[0] < l[1]:
        return l[(1, 0)]
    return l

def sort3(l):
    if l[0] < l[1]:
        if l[1] < l[2]:
            return l[(2, 1, 0)]
        elif l[0] < l[2]:
            return l[(1, 2, 0)]
        else:
            return l[(1, 0, 2)]
    elif l[1] < l[2]:
        if l[0] < l[2]:
            return l[(2, 0, 1)]
        else:
            return l[(0, 2, 1)]
    else:
        return l

sort = [None, lambda l: l, sort2, sort3]
...
    atk_rolls = sort[n_atk_dice](np.random.randint(1, 7, n_atk_dice))
    def_rolls = sort[n_def_dice](np.random.randint(1, 7, n_def_dice))

В-третьих, используйте numpy для подсчета вместо создания нового списка для подсчета:

def_losses = (comp > 0).count_nonzero()

и выполнить итерацию по списку только один раз:

atk_losses = comp_ind - def_losses

В-четвертых, попробуйте применить тот же трюк для сравнений, что и для сортировки. Вместо того, чтобы использовать полностью общие сравнения numpy, вычитание массива и т. Д., Поймите, что есть два случая: comp_ind равно 1 или 2. Если вы напишете конкретный код для каждого случая, вы можете получить более быстрый код и, возможно, вообще отказаться от использования numpy.

Наконец, исследуйте генерацию случайных чисел. На самом деле это может быть ваша точка захвата. См. Например https://eli.thegreenplace.net/2018/slow-and-fast-methods-for-generating-random-integers-in-python/. Если вы можете получить решение на базе Python (без numpy) с быстрыми случайными числами или сразу сгенерировать большие партии случайных чисел, вы можете получить повышение производительности.

Предварительная обработка

Обязательно прочитайте отличный ответ superb_rain.

Следующий код предназначен для предварительной обработки. Он просто перебирает каждую конфигурацию атаки и защиты и вычисляет совокупную вероятность того, что атакующему удастся убить 0, 1 или 2 солдат защиты.

Он медленный, но это не проблема, так как он должен запускаться только один раз и выводить распределение вероятностей, которое вы можете использовать в своем коде.

from itertools import product
from collections import Counter

D6 = [1, 2, 3, 4, 5, 6]

probabilities = {}

for n_atk_dice in range(1, 4):
    for n_def_dice in range(1, 3):
        attacker_kills = Counter()
        for attack in product(D6, repeat=n_atk_dice):
            attack = sorted(attack, reverse=True)
            for defense in product(D6, repeat=n_def_dice):
                defense = sorted(defense, reverse=True)
                result = sum(1 for a,d in zip(attack, defense) if a > d)
                attacker_kills[result] +=1
        probabilities[(n_atk_dice, n_def_dice)] = [
            attacker_kills[0],
            attacker_kills[0] + attacker_kills[1],
            attacker_kills[0] + attacker_kills[1] + attacker_kills[2]
            ]

import pprint
pprint.pprint(probabilities)

probabilities сейчас:

{(1, 1): [21, 36, 36],
 (1, 2): [161, 216, 216],
 (2, 1): [91, 216, 216],
 (2, 2): [581, 1001, 1296],
 (3, 1): [441, 1296, 1296],
 (3, 2): [2275, 4886, 7776]}

Это вся необходимая информация, и вам больше не нужно будет сортировать массив. Вы можете сохранить код в отдельном скрипте и просто использовать это буквальное определение в своем коде. Вы можете проверить значения с помощью других источников (например, https://web.stanford.edu/~guertin/risk.notes.html).

Использовать

С участием random.choices

Например, для 3 vs 2:

import random
random.choices([0, 1, 2], cum_weights=probabilities[(3, 2)])
# => Either [0], [1] or [2]

Будет вероятность 2275/7776, что атака потеряет 2 солдат, (4886 — 2275) / 7776 шанс, что обе стороны потеряют 1 солдата, и (7776-4886) / 7776 шанс, что защита потеряет 2 солдат.

Для 1 против 2:

random.choices([0, 1, 2], cum_weights=probabilities[(1, 2)])
# => [0] or [1]

Поскольку совокупные веса равны [161, 216, 216], есть 0% шанс, что защита потеряет 2 солдат. Либо атака теряет солдата (с вероятностью 161/216), либо защита теряет одного (с вероятностью 55/216).

С участием random.random()

Вы также можете определить probabilities сюда:

total = sum(attacker_kills.values())
probabilities[(n_atk_dice, n_def_dice)] = [
    attacker_kills[0] / total,
    (attacker_kills[0] + attacker_kills[1]) / total
]

Результат становится:

{(1, 1): [0.5833333333333334, 1.0],
 (1, 2): [0.7453703703703703, 1.0],
 (2, 1): [0.4212962962962963, 1.0],
 (2, 2): [0.44830246913580246, 0.7723765432098766],
 (3, 1): [0.3402777777777778, 1.0],
 (3, 2): [0.2925668724279835, 0.628343621399177]}

Затем вы можете просто получить случайное число от 0,0 до 0,99999999999 (с random.random()) и сравните его с двумя значениями.

• Если случайное число меньше первого числа: защита не теряет солдат.
• Если случайное число находится между обоими числами, защита теряет 1 солдата.
• Если случайное число больше второго: защита теряет 2 солдат.

Если защита проигрывает x солдаты, нападающий проигрывает min(n_atk_dice, n_def_dice) - x солдаты.

Цепи Маркова

Ради интереса я попытался использовать нескуммированные вероятности для определения Цепь Маркова:

# pip install PyDTMC
# see https://pypi.org/project/PyDTMC/
from pydtmc import MarkovChain, plot_graph

N = 30

probabilities = {
 (1, 1): [0.5833333333333334, 0.4166666666666667, 0.0],
 (1, 2): [0.7453703703703703, 0.25462962962962965, 0.0],
 (2, 1): [0.4212962962962963, 0.5787037037037037, 0.0],
 (2, 2): [0.44830246913580246, 0.32407407407407407, 0.22762345679012347],
 (3, 1): [0.3402777777777778, 0.6597222222222222, 0.0],
 (3, 2): [0.2925668724279835, 0.3357767489711934, 0.37165637860082307]}

states = [(a, b) for a in range(N) for b in range(N)]

#NOTE: A sparse matrix would be a good idea for large N
p = [[0 for _ in range(N * N + 2)] for _ in range(N * N + 2)]

p[-1][-1] = 1.0 # Absorbing state 'defense wins'
p[-2][-2] = 1.0 # Absorbing state: 'attack_wins'

def state_id(a, b):
    return a * N + b

for a, b in states:
    i = state_id(a, b)
    if a == 0:
        p[i][-1] = 1.0 # defense wins
    elif b == 0:
        p[i][-2] = 1.0 # attack wins
    else:
        a_dice = min(a, 3)
        b_dice = min(b, 2)
        d = min(a_dice, b_dice)
        p0, p1, p2 = probabilities[(a_dice, b_dice)]
        p[i][state_id(a-d,b)] = p0
        p[i][state_id(a-(d-1),b-1)] = p1
        if d == 2:
            p[i][state_id(a-(d-2),b-2)] = p2

state_names = [f'{a} vs {b}' for a, b in states] + ['attack_wins', 'defense_wins']
    
mc = MarkovChain(p, state_names)

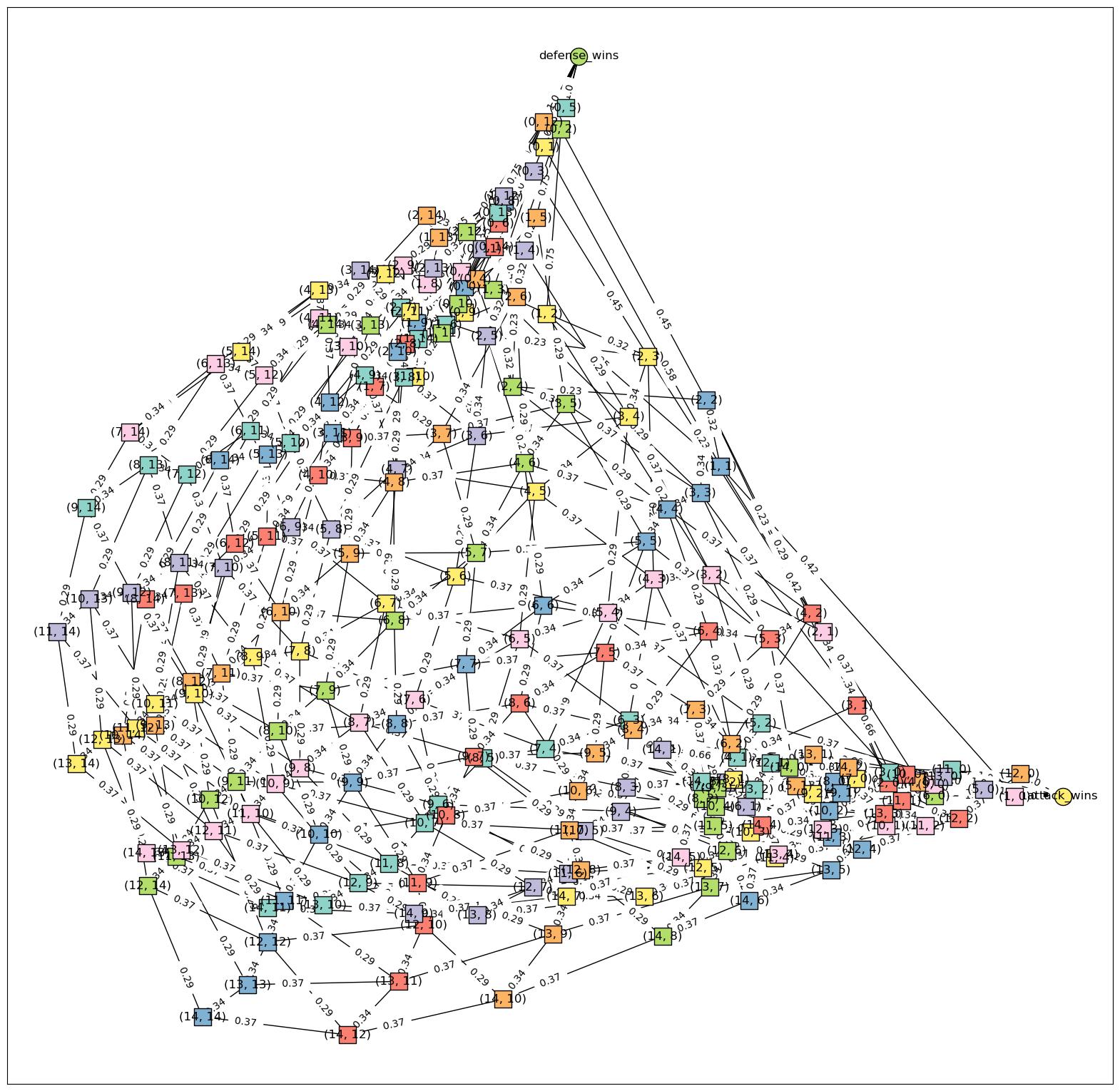
Полученные графики интересны:

import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [15, 10]
plot_graph(mc, nodes_type=False, dpi=200)

mc.absorption_probabilities — матрица, содержащая вероятности выигрыша или проигрыша в зависимости от начального состояния.

Вы можете получить вероятность того, что атакующий выиграет для заданного старта (например, 10 против 7), без какого-либо цикла:

mc.absorption_probabilities[0][state_id(10, 7)]
# 0.7998329909591375

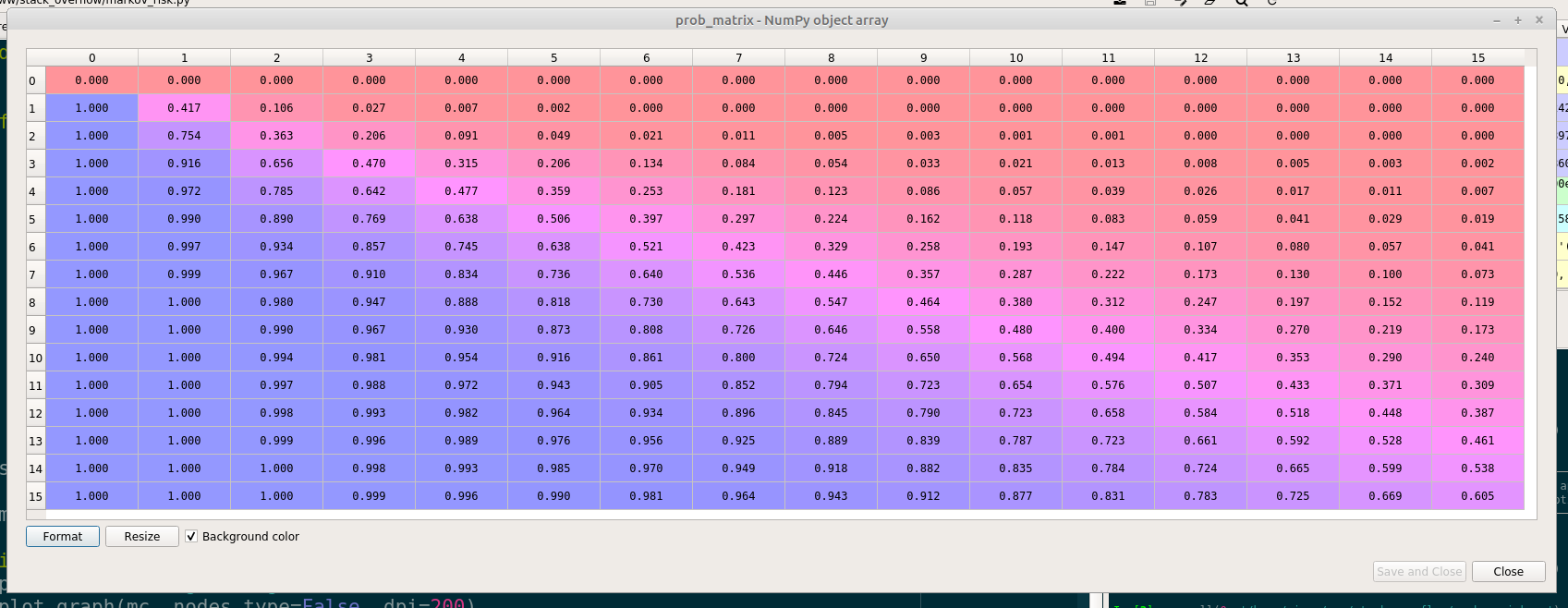
И, повторяя каждое начальное состояние, можно воссоздать представленную матрицу в этом ответе:

import numpy as np
prob_matrix = np.array([[mc.absorption_probabilities[0][state_id(b,a)]
                         for a in range(N)] for b in range(N)])

Также можно увидеть промежуточные шаги во время случайного боя:

mc.walk(20, initial_state="12 vs 9")

Он выводит:

['12 vs 7',
 '11 vs 6',
 '10 vs 5',
 '10 vs 3',
 '9 vs 2',
 '8 vs 1',
 '8 vs 0',
 'attack_wins', ....

If you profile the code without using njit, you will find that most of the time is consumed in calls to randint and sort:

atk_rolls = sort[n_atk_dice](np.random.randint (1, 7, n_atk_dice)) def_rolls = сортировать[n_def_dice](np.random.randint (1, 7, n_def_dice))

Таким образом, вместо генерации и сортировки этих случайных чисел для каждой итерации цикла вы можете предварительно сгенерировать их: сохраняя их в массиве длиной 200 (в худшем случае вам понадобится 200 строк).